Answer: The osmotic pressure is 54307.94 Torr.
Step-by-step explanation:
To calculate the concentration of solute, we use the equation for osmotic pressure, which is:

where,
 = osmotic pressure of the solution = ?
= osmotic pressure of the solution = ?
i = Van't hoff factor = 3
C = concentration of solute = 0.958 M
R = Gas constant =
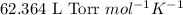
T = temperature of the solution =
![30^oC=[30+273]K=303K](https://img.qammunity.org/2020/formulas/chemistry/high-school/qgk25dipm0wmrera79tmilvyvp64mm2nlu.png)
Putting values in above equation, we get:

Hence, the osmotic pressure is 54307.94 Torr.