Answer:
C
Explanation:
EFGH is a kite, so EF ≅ FG and EH ≅ HG.
The area of the kite consists of two area of triangles EFG and EHG.
1. Area of triangle EFG:
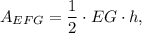
where h is the height drawn from point F to the side EG.
1. Area of triangle EHG:
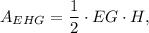
where H is the height drawn from point H to the side EG.
3. Note that
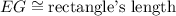
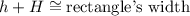
So,
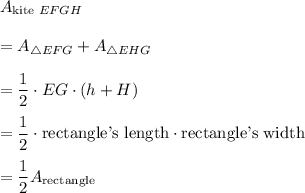
Thus, option C is true (the area of the kite doesn't depend on ratio in which points E and G divide the side)