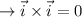Let , a, b and c be the length of three sides of triangle, represented in terms of vectors as
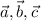 .
.
Now, vector of same Magnitude acts as normal vector to each side.
So, equation of any vector p having normal q is given by
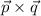
Now sum of three vector and it's normal is given as
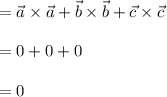
Cross product of two identical vectors is Zero.