Answer:
(a) If f and t are both even functions, product ft is even.
(b) If f and t are both odd functions, product ft is even.
(c) If f is even and t is odd, product ft is odd.
Explanation:
Even function: A function g(x) is called an even function if

Odd function: A function g(x) is called an odd function if
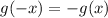
(a)
Let f and t are both even functions, then

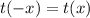
The product of both functions is
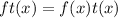

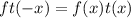

The function ft is even function.
(b)
Let f and t are both odd functions, then
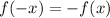
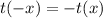
The product of both functions is
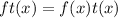

![ft(-x)=[-f(x)][-t(x)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/n3rw05zh78c97bot6xff0fvvez0ynqvnsg.png)

The function ft is even function.
(c)
Let f is even and t odd function, then

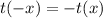
The product of both functions is
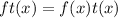

![ft(-x)=[f(x)][-t(x)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/uqglzeh8nrjrsbyk64hjkh1bsmaj3m1vxc.png)
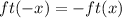
The function ft is odd function.