Question

The area of a rectangular room is 750 square feet. The width of the room is 5 feet less than the length of the room. The area of a rectangular room is 750 square feet. The width of the room is 5 feet less than the length of the room. Which equations can be used to solve for y, the length of the room? Select three options. y(y + 5) = 750 y2 – 5y = 750 750 – y(y – 5) = 0 y(y – 5) + 750 = 0 (y + 25)(y – 30) = 0

Answer 1

Answer: edge 2022. (b, c, e)

Explanation:

Answer 2

`y^(2)-5y=750`

`750-y(y-5)=0`

`(y + 25)(y -30) = 0`

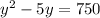
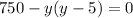
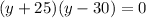
Explanation:

Givens

• The area of a rectangular room is 750 square feet.
• The width of the room is 5 feet less than the length of the room.

Let's call
`w` the width and
`l` the length. According to the problem they are related as follows

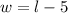`w=l-5`, because the width is 5 feet less than the lenght.

We know that the area of the room is defined as

`A=w* l`

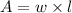
Where
`A=750 ft^(2)`

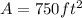
Replacing the given area and the expression, we have

`750=(l-5)l\\750=l^(2)-5l \\l^(2)-5l-750=0`

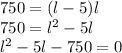
We need to find two number which product is 750 and which difference is 5, those numbers are 30 and 25.

`l^(2)-5l-750=(l-30)(l+25)`

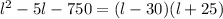
Using the zero property, we have

`l=30\\l=-25`

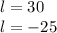
Where only the positive number makes sense to the problem because a negative length doesn't make any sense.

Therefore, the length of the room is 30 feet.

Also, the right answers are the second choice where
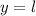`y=l`, the third choice and the last choice.