Question

Which recursive formula can be used to generate the sequence below, where f(1) = 6 and n ≥ 1?

6, 1, –4, –9, –14, …

f (n + 1) = f(n) + 5
f (n + 1) = f(n) – 5
f (n) = f(n + 1 ) – 5
f (n + 1) = –5f(n)

Answer 1

b

Explanation:

Answer 2

Answer: The correct option is

(B)
`f(n+1)=f(n)-5.`

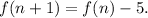
Step-by-step explanation: We are given to select the correct recursive formula that can be used to generate the following sequence :

`f(1)=6,n\geq1,\\\\6,1,-4,-9,-14,...`

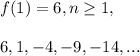
Let f(n) denote the nth term of the given sequence. Then, we note that

`f(1)=6,\\\\f(2)=1=6-5=f(1)-5,\\\\f(3)=-4=1-5=f(2)-5,\\\\f(4)=-9=-4-5=f(3)-5,\\\\f(5)=-14=-9-5=f(4)-5,\cdots`

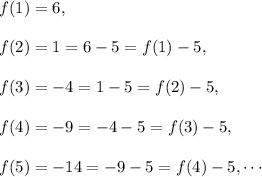
Therefore, the recursive formula can be written as :

`f(n+1)=f(n)-5.`

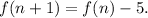
Thus, the required recursive formula is
`f(n+1)=f(n)-5.`

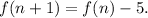
Option (B) is CORRECT.