Question

Question 1: Describe in words the region of double-struck R3 represented by the equation: x2 + z2 ≤ 36.

Question 2: Here x2 + z2 ≤ 36, or equivalently x2 + z2 ≤ 6, describes the set of all points in double-struck R3 whose distance from the -axis is a _______.

Answer 1

Explanation:

1) i will asume x2 and z2 are squares here.

ok, here we only have restrictions to x and z, so y can take all the values in R.

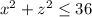`x^(2)  + z^(2)  \leq 36` is a circle of radius 6, you can see this if for example we set z = 0, then x goes from -6 to 6, the same if we set x = 0 then z goes from -6 to 6.

and the equation
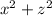`x^(2)  + z^(2) \\` describes a circle.

So here, the region is the solid cylinder of radius 6, where the Y axis is also the axis of the cylinder.

2) you tipped the same inequality but different numbers in the right side, here i think you are saying that the inequalities describes the set of all points whose distance from the y-axis is equal or less tan 6.