Question

How can you determine the coordinates of any image that is dilated with the center of dilation at the origin without graphing? Explain your reasoning.

Answer 1

The image of point (x , y) by dilation with center origin and scale factor k is (kx , ky)

Explanation:

* Lets talk about dilation

- A dilation is a transformation that changes the size of a figure.

- It can become larger or smaller, but the shape of the

figure does not change.

- The scale factor, measures how much larger or smaller

the image will be

- If the scale factor greater than 1, then the image will be larger

- If the scale factor between 0 and 1, then the image will be smaller

* In a problem of dilation

∵ The center of dilation is the origin

∵ The scale factor of dilation is k

∵ The point is (x , y)

- In dilation with center origin and scale factor k to find the image

of the point multiply each coordinates of the point by the scale

factor k because the distance d between the point and the

origin will be equal kd which is the distance between the origin

and the image of the point d is depending on the coordinates

of the point

∴ The image of point (x , y) by dilation with center origin and

scale factor k is (kx , ky)

* Ex: If point A is (3 , 4)

∵ The distance from the origin to point A =
`\sqrt{(3)^(2)+(4)^(2)}=√(9+16)=√(25)=5`

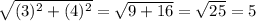
∵ The scale factor of dilation is 2 and the center is the origin

∴ The image of A is A' = (3 × 2 , 4 × 2) = (6 , 8)

∵ The distance from the origin to point A' =
`\sqrt{(6)^(2)+(8)^(2)}=√(36+64)=√(100)=10`

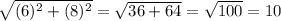
∵ 10 ÷ 5 = 2 which is the value of the scale factor

∴ The image of point (x , y) by dilation with center origin and

scale factor k is (kx , ky)