Question

Ted Williams hits a baseball with an initial velocity of 120 miles per hour (176 ft/s) at an angle of ? = 35 degrees to the horizontal. The ball is struck 3 feet above home plate. You watch as the ball goes over the outfield wall 420 feet away and lands in the bleachers. After you congratulate Ted on his hit he tells you, 'You think that was something, if there was no air resistance I could have hit that ball clear out of the stadium!'

Assuming Ted is correct, what is the maximum height of the stadium at its back wall x = 565 feet from home plate, such that the ball would just pass over it?
You may need:
9.8 m/s2 = 32.2 ft/s2
1 mile = 5280 ft
h = feet

Answer 1

The maximum height of the stadium is 151.3 feet

Step-by-step explanation:

Please see the attached figure for a graphical description of the problem

The equation that describes a parabolic motion is:

r = (x0 + v0 t cos θ ; y0 + v0 t sin θ + 1/2 g t²)

where:

r = position vector

x0 = initial horizontal position

v0 = initial speed

θ = launching angle

y0 = initial vertical position

t = time

g = vertical acceleration due to gravity.

First, let´s find how much time the ball travels to reach a horizontal displacement of 565 feet.

The module of the rx vector (see figure) is the distance from home to the back wall of the stadium:

rx =(x0 + v0 t cos θ ; 0)

module of rx =
`\sqrt{(x0 + v0 t cos\alpha)^(2)}` = 565 feet

565 feet = x0 + v0 t cos θ (considering home as initial position, x0 = 0)

565 feet / v0 cos θ = t

565 feet / 176 feet/s cos 35° = t

t = 3.92 s

With this new data, we can now calculate the module of the y-component of the vector r at time t = 3.92, which is the time at which the ball travels 565 feet in the horizontal.

The y-component of vector r is:

ry =(0 ; y0 + v0 t sin θ + 1/2 g t²)

module of ry =
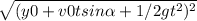`\sqrt{(y0 + v0 t sin\alpha + 1/2 g t^(2))^(2) }` = back wall height (h)

h = y0 + v0 t sin θ + 1/2 g t²

Replacing with the data:

h = 3 ft + 176 ft/s * 3.92 s* sin 35° + 1/2 * (-32.2 ft/s²) * (3.92 s)²

h = 151.3 ft