Let, the geometric sequence is such that, value of common ratio is less than 1.
The Sequence is
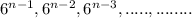
The Geometric Squence is infinite geometric sequence, as there are uncountable terms in the sequence.
⇒So, From
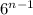 , to infinity, there will be n terms which will be integers when , n≥1.
, to infinity, there will be n terms which will be integers when , n≥1.
⇒Put, n=1,
Number of terms which are Positive Integers =1 which is
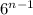 .
.
⇒When, n=2
Number of terms which are Positive Integers =2 which is
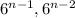 .
.
⇒When, n=3
Number of terms which are Positive Integers =3, which is
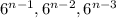 .
.
..........
So,⇒ when , n=r
Number of terms which are Positive Integers =r, which is
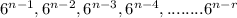 .
.