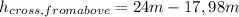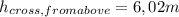Question

2.86 A ball is dropped from rest from the top of a cliff that is 24 m high. From ground level, a second ball is thrown straight upward at the same instant that the first ball is dropped. The initial speed of the second ball is exactly the same as that of the first ball in the instant just before it hits the ground. (Assume no air resistance. The motion of each ball is exactly the reverse of each other.) Determine how far below the top of the cliff the balls cross paths (are at the same position).

Answer 1

Distance Below the top = 6,02 m

Step-by-step explanation:

To get the Final velocity of the first ball (that will be the intial velocity of the second) you need to solve the kinematic equation for Velocity:

(1)
`V_(1f) =V_(1O) - gt`

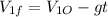
As the ball is dropped from rest
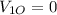`V_(1O) = 0`, so:

(2)
`V_(1f) = - gt`

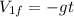
Note that the velocity is going to be negative as the ball is going down. To get the time it would take the ball to reach de base you can use the kinematic equation for position:

(3)
`h_(1) = h_(1O) + V_(1O) *t - (1)/(2) gt^(2)`

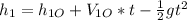
We need the answer when h=0, and from the initial conditions
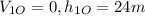`V_(1O) = 0, h_(1O) = 24m`, you get:

(4)
`24m = (1)/(2) gt_(1f)^(2)`

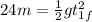
Solving for t, with
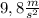`9,8(m)/(s^(2))` and :

(5)
`t_(1f) = \sqrt{(24m*2)/(g) } = 2,21 s`

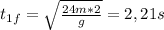
Replacing this time in (2), the final velocity is:

(6)
`V_(1f) = -21,66 (m)/(s)`

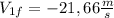
So the initial velocity of ball 2 is equial to this but oppossite in direction so:
`V_(2O)= -V_(1f) = 21,66 (m)/(s)`

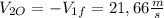
The general position equation for ball 2 is (considering
`h_(2O) = 0` :

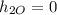(7)
`h_(2) = V_(2O) *t - (1)/(2) gt^(2)`

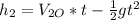
They cross paths when
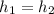`h_(1)=h_(2)` so:

(8)
`h_(1O) - (1)/(2) gt^(2) = V_(2O) *t - (1)/(2) gt^(2)`

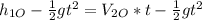
Rearranging:

(9)
`t_(cross) =(h_(1O))/(V_(2O) )`

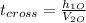
Replacing values:

`t_(cross) = 1,108 s`

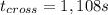
To get the absolute position replace
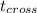`t_(cross)` on equation (3) or (7):

`h_(cross) = 17,98 m`

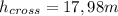
To get it below the top of te cliff:

`h_(cross, from above) = 24 m - 17,98 m`

`h_(cross, from above) = 6,02 m`