Answer:
a)
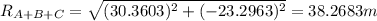
b) Θ=
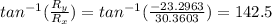 º
º
c)
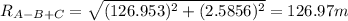
d) β=
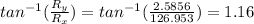 º
º
e)
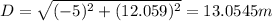
f) ∅=
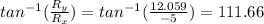 º
º
Step-by-step explanation:
First of all, we need to establish our vectors and it's directions:
A=50 m, 30º
B=50 m, 195º
C=50 m, 315º
Now that we have the three vectors, we need to calculate the x and y components:
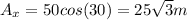
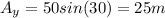
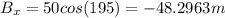
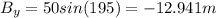
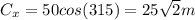
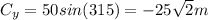
Now, that we have the components, we can calculate the resultant's components:
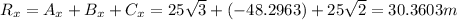
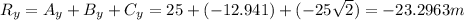
To find the resultant of the vector A+B+C we need to do the following steps:
a)
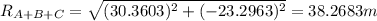
To find the angle it's necessary to use
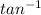 :
:
b) Θ=
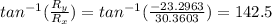 º
º
To find the resultant of the vector A-B+C we need to do the following steps:
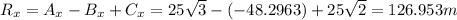
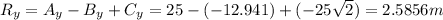
c)
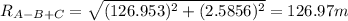
To find the angle it's necessary to use
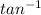 :
:
d) β=
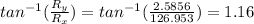 º
º
To find D=A+B it's important to follow the following steps:
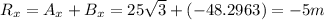
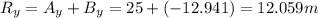
e)
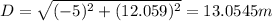
f) ∅=
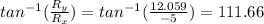 º
º