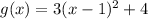Question

Help please 1. Describe the transformations necessary to transform the graph of

f(x) to that of g(x)
f(x) = x² and g(x) = 3(x - 1)² + 4

Answer 1

Here are all the steps, and what they do:

STEP 1: HORIZONTAL TRANSLATION

We transform

`x^2\mapsto (x-1)^2`

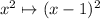
The general transformation is

`f(x)\mapsto f(x+k)`

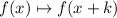
These transformations translate the graph horizontally, k units to the left if k>0, k units to the right if k<0.

In this case, k = -1, so we translate the original graph 1 unit to the right.

STEP 2: VERTICAL STRETCH

We transform

`(x-1)^2\mapsto 3(x-1)^2`

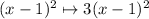
The general transformation is

`f(x)\mapsto kf(x)`

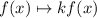
These transformations stretch the graph vertically. The graph expands if |k|>1, while it shrinks if 0<|k|<1. If k is negative, we also reflect the graph with respect to the x axis.

In this case, k = 3, so we stretch the graph vertically by a factor 3.

STEP 3: VERTICAL TRANSLATION

We transform

`3(x-1)^2\mapsto 3(x-1)^2+4`

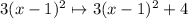
The general transformation is

`f(x)\mapsto f(x)+k`

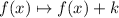
These transformations translate the graph vertically, k units up if k>0, k units down if k<0.

In this case, k = 4, so we translate the graph 4 units up.

So, we start from the original graph of
`f(x)=x^2` and we:

• Translate it 1 unit to the right
• Stretch it vertically by a factor 3
• Translate it 4 units up

(the order is important!)

to get the graph of
`g(x)=3(x-1)^2+4`