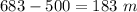Answer:
Option A) 183 meters
Explanation:
see the attached figure to better understand the problem
step 1
Find the distance BC
we know that
In the right triangle ABC
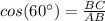 ----> adjacent side divided by the hypotenuse
----> adjacent side divided by the hypotenuse
Remember that
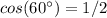
substitute the values
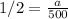
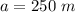
step 2
Find the distance AC
In the right triangle ABC
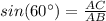 ----> opposite side divided by the hypotenuse
----> opposite side divided by the hypotenuse
Remember that
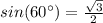
substitute the values
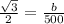
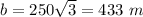
step 3
Find the distance AC+CB
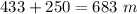
Subtract the distance AB from 683 m