Question

To reduce laboratory​ costs, water samples from six public swimming pools are combined for one test for the presence of bacteria. Further testing is done only if the combined sample tests positive. Based on past​ results, there is a 0.004 probability of finding bacteria in a public swimming area. Find the probability that a combined sample from six public swimming areas will reveal the presence of bacteria. Is the probability low enough so that further testing of the individual samples is rarely​ necessary?

Answer 1

The probability that a combined sample from six public swimming areas will reveal the presence of bacteria = 0.02376

Explanation:

As per the given question

We have given that from six public swimming pools, the probability of finding bacteria in a swimming pool = 0.004

Therefore,

P(Swimming pool has bacteria ) = 0.004

P(That swimming pool does not show the presence of Bacteria) = 1 - 0.004 = 0.996

Probability that all six pools test negative

`=(1-p)^(6)`

`=0.996^(6)`

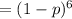
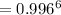
= 0.97624

Probability that at least one pool tests positive

= 1 - 0.97624

= 0.02376

Therefore,

The probability that a combined sample from six public swimming areas will reveal the presence of bacteria = 0.02376

Yes the probability is low enough so that further testing of the individual samples is rarely​ necessary.