Question

How many complex roots does the equation below have?

x 6 + x 3 + 1 = 0

Answer 1

Consider the change of variable

`x^3=t`

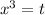
The equation becomes

`t^2+t+1=0`

This equation has solutions

`t=(-1\pm√(1-4))/(2)=(-1\pm√(-3))/(2)`

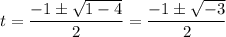
Now we should find the corresponding x values by reverting the variable change:

`x^3=t \implies x = \sqrt[3]{t}`

Using complex numbers, every number has three cubic roots, so the solutions are

`x_(1,2,3)=\sqrt[3]{(-1+√(-3))/(2)},\quad x_(4,5,6)=\sqrt[3]{(-1-√(-3))/(2)}`

So, all six roots are complex.