Question

Find P(Y|B) from the information in the table.

A 5-column table has 4 rows. The first column has entries A, B, C, Total. The second column is labeled X with entries 8, 6, 23, 37. The third column is labeled Y with entries 80, 34, 56, 170. The fourth column is labeled Z with entries 40, 45, 32, 117. The fifth column is labeled Total with entries 128, 85, 111, 324.

To the nearest tenth, what is the value of P(Y|B)?

0.2
0.3
0.4
0.5

Answer 1

C. 0.4

Explanation:

correct on edge, have a nice day:)

Answer 2

0.4

Explanation:

The table with correct formatting is attached in the image below.

We have to find P(Y | B). This is a conditional probability i.e. probability of Y given B.

The formula of conditional probability for two event A and B is:

`P(A|B)=(P(A \cap B))/(P(B))`

So, for the given case, the formula would be:

`P(Y|B)=(P(Y \cap B))/(P(B))`

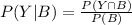
P(Y ∩ B) indicates the probability of Y and B occurring together. Y and B occur together 34 times out of total of 324, so:

`P(Y \cap B)=(34)/(324)`

P(B) indicates the probability of occurrence of B. B occurs 85 times in a total of 324. So,

`P(B)=(85)/(324)`

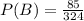
Using these values in the formula of conditional probability, we get:

`P(Y \cap B)=((34)/(324))/((85)/(324) )\\\\ =(34)/(85)\\\\ =0.4`

Thus, the value of P(Y|B) is 0.4