Question

12. Write 18(cos169° + isin169°) in rectangular form. Round numerical entries in the answer to two decimal places.

Answer 1

The rectangular form is z = -17.67 + i 3.43

Explanation:

Answer 2

The rectangular form is z = -17.67 + i 3.43

Explanation:

* Lets explain how change the modulus form to the rectangular form

- The rectangular form of a complex number is given by

z = a + bi , where

a = r cos Ф and b = r sin Ф

- The modulus form of the complex number is

z = r(cos Ф + i sin Ф) where

`r=\sqrt{a^(2)+b^(2)}`

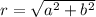
Ф =
`tan^(-1)(b)/(a)`

* Lets solve the problem

∵ z = 18(cos(169)° + i sin(169)°)

∵ z = r(cos Ф + i sin Ф)

∴ r = 18 and Ф = 169°

∵ z = a + ib , where

a = r cos Ф and b = r sin Ф

∴ a = 18 cos(169)°

∴ b = 18 sin(169)°

- Angle Ф lies in the 2nd quadrant (90° < Ф < 180°)

∵ sin(169)° is positive ⇒ (sine in the 2nd quadrant positive)

∵ cos(169)° is negative ⇒ (cosine in the 2nd quadrant is negative)

∴ a = -17.67

∴ b = 3.43

∴ z = -17.67 + i 3.43

* The rectangular form is z = -17.67 + i 3.43