Question

Which expressions are equivalent to 2(b+3c)?

Choose all answers that apply:

(Choice A)

3(b+2c)

(Choice B)

(b+3c)+(b+3c)

(Choice C)

2(b)+2(3c)

Answer 1

B. (b+3c)+(b+3c)

C. 2(b)+2(3c)

Explanation:

we have

`2(b+3c)`

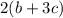
Distribute the number 2

`2(b+3c)=2b+2(3c)=2b+6c`

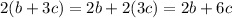
Verify each case

case A) 3(b+2c)

distribute the number 3

`3(b+2c)=3b+3(2c)=3b+6c`

`3b+6c \\eq 2b+6c`

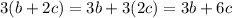
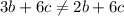
therefore

Choice A is not equivalent to the given expression

case B) (b+3c)+(b+3c)

Combine like terms

`b+3c)+(b+3c)=(b+b)=(3c+3c)=2b+6c`

`2b+6c= 2b+6c`

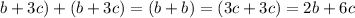
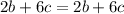
therefore

Choice B is equivalent to the given expression

case C) 2(b)+2(3c)

Multiply both terns by 2

`2(b)+2(3c)=2b+6c`

`2b+6c= 2b+6c`

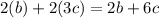
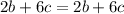
therefore

Choice C is equivalent to the given expression