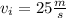Question

A golf ball is hit from ground level at an angle of 3030 degrees above ground level. The terrain is level. The ball lands 55.231255.2312 meters away. What was the initial speed of the golf ball?

Answer 1

25 m/s

Step-by-step explanation:

Angle of projection, θ = 30°

Horizontal distance, r = 55.231 m

Let u be the velocity of projection.

Use the formula of horizontal range

`R=(u^(2)Sin2\theta )/(g)`

By substituting the values, we get

`55.231=(u^(2)Sin60 )/(9.8)`

`55.231=(u^(2)* 0.866 )/(9.8)`

u = 25 m/s

thus, the initial velocity of golf ball is 25 m/s.

Answer 2

The initial speed of the golf ball was 25 m/s.

Step-by-step explanation:

To find the initial speed of a projectile motion we must first find the motion equation corresponding to each axis:

For X axis we have an Uniform Rectilinear Motion, since no forces act along it:

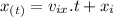`x_((t))=v_(ix).t+x_i`, where
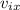`v_(ix)` stands for the initial speed component on x axis, and
`x_i` is the initial position on x axis (zero, in this case).

For Y axis we have a Constant Acceleration Motion, since the gravitational force acts along it:

`y_((t))=-(1)/(2) g.t^(2) +v_(iy).t+y_i`, where g is the acceleration of gravity,
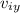`v_(iy)` stands for the initial speed component on y axis, and
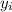`y_i` is the initial position on y axis (zero, in this case).

We can describe the initial speed's components as follow:

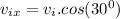`v_(ix)=v_i.cos(30^0)` and
`v_(iy)=v_i.sin(30^0)`

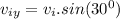
Keeping this in mind, we're just three steps away from the answer.

The first step is expressing t in terms of x:

`t=(x)/(v_i.cos(30^0))`

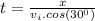
The second step is replacing this expression for t on the y axis equation:

`y_((x))=-(1)/(2) .g.((x)/(v_i.cos(30^0)) )^2+(v_i)/(v_i) (sin(30^0))/(cos(30^0)) .x`

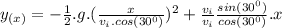
Finally, we use the fact that when x=55.2312 m the golf ball lands, it means y=0 m, and resolve the equation for
`v_i`

`0m=-(1)/(2) .9,8(m)/(s^2).((55,2312m)/(v_i.cos(30^0)) )^2+(sin(30^0))/(cos(30^0)) .55,2312m`

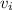
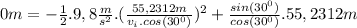
Obtaining

`v_i=25(m)/(s)`