Question

Please help me with this....................

Answer 1

C

Step-by-step explanation

inequalities of the type | x | < a, always have solutions of the form

- a < x < a

This can be extended to expressions, that is

A

- 4 < 2x - 3 < 4 ( add 3 to all 3 intervals )

- 1 < 2x < 7 (divide all intervals by 2 )

-
`(1)/(2)` < x <
`(7)/(2)`

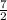
This is not the solution shown on the number line, that is

x < - 1 or x > 8

B

- 12 < x - 3 < 12 ( add 3 to all intervals )

- 9 < x < 15 ← not the required solution

--------------------------------------------------------------------------

Inequalities of the type | x | > a, always have solutions of the form

x < - a or x > a, thus

C

2y - 7 < - 9 OR 2y - 7 > 9 ( add 7 to both sides of both intervals )

2y < - 2 OR 2y > 16 ( divide both sides of both intervals by 2 )

y < - 1 OR y > 8 ← required solution

Thus C represents the solution shown on the graph

Answer 2

c

Explanation:

|2y - 7| > 9

<=> 2y - 7 > 9 or 7 - 2y < 9

<=> 2y > 16 or -2y > 2

<=> y > 8; y < -1