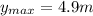Answer:
a) 9.8 m/s
b) 4.9 m
Step-by-step explanation:
This problem is a good example of Vertical motion, where the main equations for this situation are:
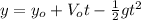 (1)
(1)
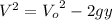 (2)
(2)
Where:
 is the height of the ball at a given time
is the height of the ball at a given time
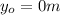 is the initial height of the ball (assuming the hand of the thrower the origin of the system)
is the initial height of the ball (assuming the hand of the thrower the origin of the system)
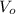 is the initial velocity of the ball
is the initial velocity of the ball
 is the final velocity of the ball
is the final velocity of the ball
 is the time it takes for the ball to make the complete movement (from the moment it is thrown until it falls back into the pitcher's hands)
is the time it takes for the ball to make the complete movement (from the moment it is thrown until it falls back into the pitcher's hands)
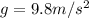 is the acceleration due to gravity
is the acceleration due to gravity
Knowing this, let's begin with the answers:
a) Initial velocity
In order to find the initial velocity
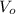 of the ball, we will use equation (1) and
of the ball, we will use equation (1) and
 , taking into account that
, taking into account that
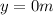 and
and
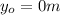 at this given time:
at this given time:
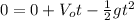 (3)
(3)
Isolating
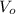 :
:
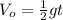 (4)
(4)
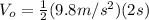 (5)
(5)
Then:
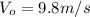 (6)
(6)
b) Maximum height
In this part, we will use equation (2), knowing the value of the height is maximum when
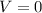 . So, we will name this height as
. So, we will name this height as
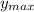 :
:
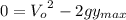 (7)
(7)
Isolating
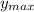 :
:
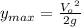 (8)
(8)
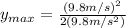 (9)
(9)
Finally: