Question

the area of the triangle shown is no more than 10 square inches. a. write an inequality that can be used to find x. b. solve the inequality from part a. c. what is the maximum height of the triangle?

Answer 1

Part a)
`(1)/(2)(4)(2x-3)\leq 10\ in^2`

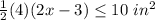
Part b) The solution of the inequality Part a) is
`x\leq 4` (see the explanation)

Part c) The maximum height of triangle is 5 inches

Explanation:

see the attached figure to better understand the problem

Part a) write an inequality that can be used to find x

we know that

The area of triangle is equal to

`A=(1)/(2)bh`

we have

`b=4\ in`

`h=(2x-3)\ in`

`A\leq 10\ in^2`

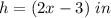
so

substitute

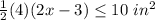`(1)/(2)(4)(2x-3)\leq 10\ in^2` ----> inequality that can can be used to find x

Part b) solve the inequality from part a

we have

`(1)/(2)(4)(2x-3)\leq 10`

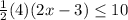
solve for x

Simplify left side

`2(2x-3)\leq 10`

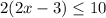
Distribute left side

`4x-6\leq 10`

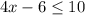
Adds 6 both sides

`4x\leq 10+6`

`4x\leq 16`

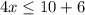
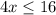
Divide by 4 both sides

`x\leq 16/4`

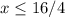
`x\leq 4` ----> solution inequality Part a)

Remember that the height cannot be negative

`h=(2x-3)\ in`

`h>0`

`(2x-3)> 0`

`2x > 3`

`x > 1.5\ in`

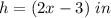
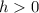
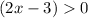
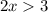
therefore

The value of x must be greater than 1.5 in and less than or equal to 4 in

Part c) what is the maximum height of the triangle?

we know that

The maximum height of triangle will be for the maximum value of x

The maximum value of x is 4 in

`h=(2x-3)\ in`

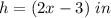
substitute for x=4 in

`h=(2(4)-3)=5\ in`

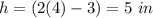
therefore

The maximum height of triangle is 5 inches