Answer:
The correct answer is: Option 1: x≤-3
Explanation:
Given inequality is:
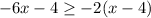
First of all, we will distribute -2 into the bracket
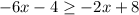
Then we will add 4 on both sides
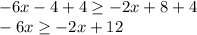
Adding 2x on both sides
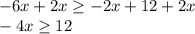
Dividing both sides by 4
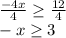
As there should be only x on the left side of the inequality we will multiply the inequality with -1.
Multiplying the inequality with -1 reverses the sign of inequality
So,
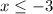
Hence,
The correct answer is: Option 1: x≤-3