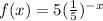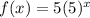Question

The function f(x) = 5One-fifth is reflected over the y-axis. Which equations represent the reflected function?

Answer 1

C. f(x) = 5(1/5)⁻ˣ , D. f(x) = 5(5)ˣ

^

|

|

That is the answer.

Right on the edge final!

I hope this helps!

- sincerelynini

Answer 2

The equations that represent the reflected functions are

`f(x)=5((1)/(5))^(-x)`

`f(x)=5(5)^(x)`

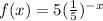
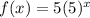
Explanation:

The correct question in the attached figure

we have the function

`f(x)=5((1)/(5))^(x)`

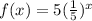
we know that

A reflection across the y-axis interchanges positive x-values with negative x-values, swapping x and −x.

therefore

`f(−x) = f(x).`

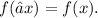
The reflection of the given function across the y-axis will be equal to

(Remember interchanges positive x-values with negative x-values)
`f(x)=5((1)/(5))^(-x)`

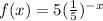
An equivalent form will be

`f(x)=5((1)/(5))^((-1)(x))=5[((1)/(5))^(-1))]^(x)=5(5)^(x)`

therefore

The equations that represent the reflected functions are

`f(x)=5((1)/(5))^(-x)`

`f(x)=5(5)^(x)`