Answer:
P(3 or more of the tickets have popcorn coupons) = 0.989
Explanation:
The probability of buying a movie ticket with a popcorn coupon is 0.608
p = 0.608
The probability of buying a movie ticket without a popcorn coupon is q
q = 1 - p = 1 - 0.608 = 0.392
If you buy 10 movie tickets, n = 10
The probability that 3 or more of the tickets have popcorn coupons.
X = 3,4,5,6,7,8,9,10
Using Binomial distribution,
p = Success , q = failure, n = number of trial , r = X
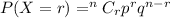
For X = 3,4,5,6,7,8,9,10
Let E be probability 3 or more of the tickets have popcorn coupons.
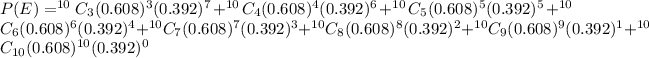
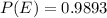
Now round to 3 decimal place.
P(3 or more of the tickets have popcorn coupons) = 0.989