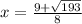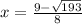Answer:
Part A)
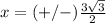
Part B)
 and
and

Part C)
 and
and

Part D)
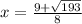 and
and
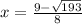
Explanation:
Part A) we have
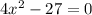
we know that
The square root property states that if we have an equation with a perfect square on one side and a number on the other side, then we can take the square root of both sides and add a plus or minus sign to the side with the number and solve the equation.
isolate the term that contains the squared variable
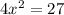
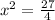
take the square root of both sides
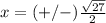
simplify
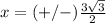
Part B) we have
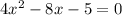
Using the quadratic equation
The formula to solve a quadratic equation of the form
 is
is

in this problem we have
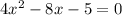
so
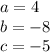
substitute in the formula
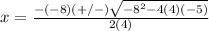
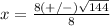
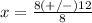
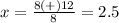
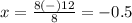
Part C) we have
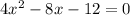
Using Factoring
Simplify the expression first
Divide by 4 both sides
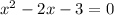
Find two numbers a and b such that
a+b=-2
ab=-3
Solve the system by graphing
The solution is a=1, b=-3
see the attached figure
so
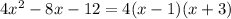
The solutions are
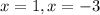
Part D) we have
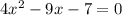
Solve by completing the square
Group terms that contain the same variable, and move the constant to the opposite side of the equation

Factor the leading coefficient
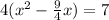
Complete the square. Remember to balance the equation by adding the same constants to each side
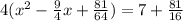
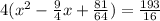
Rewrite as perfect squares
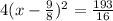
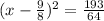
take square root both sides