Question

Ms. Garza invested $50,000 in three different accounts. She invested three times as

much money in an account that paid 8% interest than an account that paid 10% interest.
The third account earned 12% interest. If she earned a total of $5160 in interest in a year,
how much did she invest in each account?

Answer 1

The amount invested in the account that paid 8% was $18,000

The amount invested in the account that paid 10% was $6,000

The amount invested in the account that paid 12% was $26,000

Explanation:

Let

3x -----> the amount invested in the account that paid 8%

x -----> the amount invested in the account that paid 10%

$50,000-4x ----> the amount invested in the account that paid 12%

in this problem we have

`8\%=8/100=0.08\\10\%=10/100=0.10\\12\%=12/100=0.12`

we know that

`3x(0.08)+x(0.10)+(50,000-4x)(0.12)=5,160`

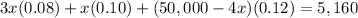
Solve for x

`0.24x+0.10x+6,000-0.48x=5,160`

`0.48x-0.24x-0.10x=6,000-5,160`

`0.14x=840`

`x=\$6,000`

`3x=\$18,000`

`\$50,000-4x=\$26,000`

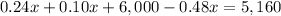
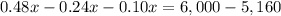
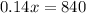
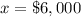
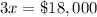
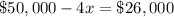
therefore

The amount invested in the account that paid 8% was $18,000

The amount invested in the account that paid 10% was $6,000

The amount invested in the account that paid 12% was $26,000