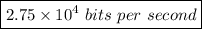Question

An analogue sensor signal is sampled every 0.4ms to convert it into a digital representation. What is the corresponding sampling rate?

According to the Sampling Theorem (Section 3.3.1), for this sampling rate value, what will be the highest frequency in the digital representation, assuming the lowest frequency in the sensor signal is very close to zero.

If each sample is quantised into 2048 levels, what will be the resulting bit-rate, giving your answer in scientific notation to 2 decimal places?

Hint: firstly, you need to calculate the number of bits per sample that produces 2048 quantisation levels

Answer 1

Hello! It will be a pleasure to help you!

So let's get started:

PART 1.

An analogue sensor signal is sampled every 0.4ms to convert it into a digital representation. What is the corresponding sampling rate?

Sampling is simply a reduction of a continuous time signal to a discrete time signal. Here we know that an analogue sensor is sampled every
`0.4ms` to convert it into a digital representation. So sampling rate, also called the sampling frequency or
`f_(s)`, is the average number of samples obtained in one second, that is, samples per second:

`f_(s)=(1)/(T)`

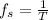
Since we know:

`T=0.4ms`

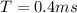
Then, the sampling rate is:

`f_(s)=(1)/(0.4ms) \\ \\ f_(s)=2,500 \ samples \ per \ second \\ \\ Or: \\ \\ \boxed{f_(s)=2.5kS/s}`

PART 2.

According to the Sampling Theorem, for this sampling rate value, what will be the highest frequency in the digital representation, assuming the lowest frequency in the sensor signal is very close to zero.

Sampling Theorem (Nyquist Theorem) States:

A continuous time signal can be completely represented in its samples and recovered back, if the sampling frequency
`f_(s)` is greater than or equal to twice frequency component of the message signal.

In other words:

`f_(s)\geq 2f_(m)`

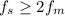
So, the highest frequency in the digital representation will be:

`f_(m)=(2500)/(2) \\ \\ \boxed{f_(m)=1.25kHz}`

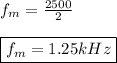
PART 3.

If each sample is quantised into 2048 levels, what will be the resulting bit-rate, giving your answer in scientific notation to 2 decimal places?

Everything is Ok up to this point! But let me explain something. We do all these things in order to get a faithful reproduction of the digital signal. So the Analog-to-Digital Conversion (ADC) allows us to do that.

In this final part, each sample is quantised to 2048 levels, so this number can be written as:

`2048=2^(11)`

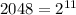
That is, there are
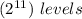`(2^(11)) \ levels`, in other words, it takes:

`11 \ bits \ per \ sample`

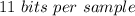
Finally, the resulting bit-rate is:

`11 * 2500 \\ \\ =27500 \ bits \ per \ second`

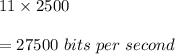
In scientific notation to two decimal places:

`\boxed{2.75 * 10^4 \ bits \ per \ second}`