Question

Write the equation of a line that is perpendicular to y=7x−2 and passes through the point (14,8).(1 point) y=7x−90 y=10x−17 y=−17x+1067 y=−17x+10

Answer 1

y=−17x+10

Explanation:

shorter version

Answer 2

`\huge\boxed{y=-(1)/(7)x+ 10}`

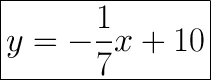
Explanation:

In order to find the equation of this line, we need to note two things.

• A) The slope of two lines that are perpendicular will be opposite reciprocals (that is, multiplying them gets us -1.)
• B) We can substitute a point inside an incomplete equation to try and find a missing value.

So first, let's find the opposite reciprocal of 7 which will be the slope to this equation.

• Reciprocal of 7:
  `(1)/(7)`
• Opposite of
  `(1)/(7)`:
  `-(1)/(7)`

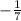
So the slope of this line will be
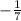`-(1)/(7)`. The y-intercept will change, and we can substitute what we know into the equation
`y=mx+b`.

`y = -(1)/(7)x+b`

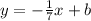
Now, we can substitute a point on the graph (14, 8) into this equation to find b.

• 
  `8 = -(1)/(7) \cdot 14 + b`
• 
  `8 = -(14)/(7) + b`
• 
  `8 = -2 + b`
• 
  `b = 10`

Now that we know the y-intercept, we can finish off our equation by plugging that in.

`y = -(1)/(7)x + 10`

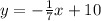
Hope this helped!