Question

The position of a model train, in feet along a railroad track, is given by

s(t) = 2.5t + 14
after t seconds.
(a) How fast is the train moving?
ft/sec
(b) Where is the train after 4 seconds?
241 feet along the track
Enter an exact number.
(c) When will the train be 29 feet along the track?
t=
sec

Answer 1

Part a) The speed is
`2.5(ft)/(sec)`

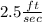
Part b) After 4 seconds the trains is 24 ft along the track

Part c)
`t=6\ sec`

Explanation:

we have

`s(t)=2.5t+14`

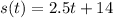
This is the equation of a line in slope intercept form

where

s(t) is the position of a model train in feet

t is the time in seconds

Part a) How fast is the train moving?

The speed of the train is equal to the slope of the linear equation so

The slope m is equal to

`m=2.5(ft)/(sec)`

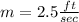
therefore

The speed is
`2.5(ft)/(sec)`

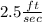
Part b) Where is the train after 4 seconds?

For t=4 sec

substitute the value of t in the equation and solve for s

`s(4)=2.5(4)+14=24\ ft`

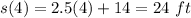
therefore

After 4 seconds the trains is 24 ft along the track

Part c) When will the train be 29 feet along the track?

For s(t)=29 ft

Substitute the value of s(t) in the equation and solve for t

`29=2.5t+14`

subtract 14 both sides

`29-14=2.5t`

`15=2.5t`

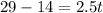
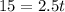
Divide by 2.5 both sides

`6=t`

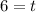
rewrite

`t=6\ sec`