Question

A 2000 gram sample of radioactive

matter will completely decay (be
undetectable) in 20 hours. There
exists a set of ordered pairs (t, m),
where t is the amount of time in hours
that the substance has been decaying,
and m is the mass in grams that has
decayed.
If t > 0, what is the range of m?

Answer 1

The range is 0 < m < 2000 when t > 0

Explanation:

* Lets explain how to solve the problem

- The exponential function is
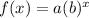`f(x)= a(b)^(x)` , where

a is the initial amount and b is the growth factor

- If b > 1, then it is exponential growth function

- If 0 < b < 1, then it is exponential decay function

* Lets solve the problem

- A 2000 gram sample of radioactive matter will completely decay

(be undetectable) in 20 hours

- There is a set of ordered pairs (t , m) exists, where t is the amount

of time in hours that the substance has been decaying and m is

the mass in grams that has decayed

∵ We can represent this situation by an exponential decay function

∴
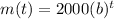`m(t)= 2000(b)^(t)` , where b is the growth factor which is

greater than zero and less than 1 , t is the lime in hours and

m(t) is the mass of the substance in gram

- In any function the domain is the value of x and the range is

the value of y

∵ In the function the domain is t and the range is m

∵ When t = 0 then m = 2000 ⇒ initial amount

∵ When t = 20 then m will be closed to zero

∴ The domain of the function is 0 < t < 20

∴ The range of the function is 0 < m < 2000

* The range is 0 < m < 2000 when t > 0