Answer:
a) { x : x = 2n + 1 ∀ n ∈ N where 50 ≤ n ≤ 99 }
b) {(x,y) :
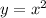 ∀ x ∈ R, y∈ R}
∀ x ∈ R, y∈ R}
Explanation:
Set builder form of a set is representation of the set in symbol and word inside {}.
a) All odd numbers between 100 and 200,
∵ every odd number is in the form of 2n + 1 where n ∈ N,
Also, the odd numbers between 100 and 200 are,
101, ....199
If 2n + 1 = 101
⇒ 2n = 100 ⇒ n = 50
If 2n + 1 = 199
⇒ 2n = 198 ⇒ n = 99
Then the set would be,
{ x : x = 2n + 1 ∀ n ∈ N where 50 ≤ n ≤ 99 }
b) All points on the graph of the function
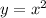 ,
,
Since, both range and domain of the function are 'Set of all real numbers'
⇒ x ∈ R, y ∈ R,
Also, (x,y) that shows the relation
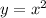 will belong to the function,
will belong to the function,
Hence, the required set builder form would be,
{(x,y) :
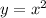 ∀ x ∈ R, y∈ R}
∀ x ∈ R, y∈ R}