Question

1. Among all simple graphs with 20 vertices, determine (with justification) the minimum possible and the maximum possible number of edges such a graph could have.

Answer 1

Minimum possible edges is 19,

Maximum possible edges is 190.

Explanation:

∵ When n vertices is joined by edges,

The minimum number of edges = n - 1 ( i.e. they are making a unique path in which first and last vertex are joined with only one vertex while the other vertices are joined with two vertices only )

Also, if the number of edges < n - 1 then the graph would be disconnected ,

While, the maximum number of edges =
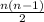`(n(n-1))/(2)` ( i.e. every vertex is joined with every vertex )

Here, n = 20,

So, the minimum possible edges = 20 - 1 = 19,

And, maximum possible edges =
`(20(20-1))/(2)`

=
`(20* 19)/(2)`

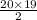
= 10 × 19

= 190