Question

Let X be a set of size 20 and A CX be of size 10. (a) How many sets B are there that satisfy A Ç B Ç X? (b) How many sets B are there such that A and B are not disjoint? Show your reasoning in both cases. You may leave your answer as an expression (eg. 510 + 3(202).)

Answer 1

(a) Number of sets B given that

• A⊆B⊆C: 2¹⁰. (That is: A is a subset of B, B is a subset of C. B might be equal to C)
• A⊂B⊂C: 2¹⁰ - 2. (That is: A is a proper subset of B, B is a proper subset of C. B≠C)

(b) Number of sets B given that set A and set B are disjoint, and that set B is a subset of set X: 2²⁰ - 2¹⁰.

Explanation:

(a)

Let
`x_1, x_2, \cdots, x_(20)` denote the 20 elements of set X.

Let
`x_1, x_2, \cdots, x_(10)` denote elements of set X that are also part of set A.

For set A to be a subset of set B, each element in set A must also be present in set B. In other words, set B should also contain
`x_1, x_2, \cdots, x_(10)`.

For set B to be a subset of set C, all elements of set B also need to be in set C. In other words, all the elements of set B should come from
`x_1, x_2, \cdots, x_(20)`.

.

For each element that might be in set B, there are two possibilities: either the element is in set B or it is not in set B. There are ten such elements. There are thus
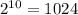`2^(10) = 1024` possibilities for set B.

In case the question connected set A and B, and set B and C using the symbol ⊂ (proper subset of) instead of ⊆, A ≠ B and B ≠ C. Two possibilities will need to be eliminated: B contains all ten "maybe" elements or B contains none of the ten "maybe" elements. That leaves
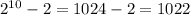`2^(10) -2 = 1024 - 2 = 1022` possibilities.

(b)

Set A and set B are disjoint if none of the elements in set A are also in set B, and none of the elements in set B are in set A.

Start by considering the case when set A and set B are indeed disjoint.

.

Set B might be an empty set. Once again, for each element that might be in set B, there are two possibilities: either the element is in set B or it is not in set B. There are ten such elements. There are thus
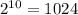`2^(10) = 1024` possibilities for a set B that is disjoint with set A.

There are 20 elements in X so that's
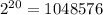`2^(20) = 1048576` possibilities for B ⊆ X if there's no restriction on B. However, since B cannot be disjoint with set A, there's only
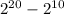`2^(20) - 2^(10)` possibilities left.