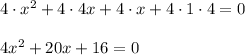Answer:
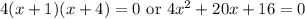
Explanation:
The quadratic equation can be written in two ways:
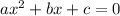
or
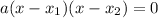
where
 is the leading coefficient and
is the leading coefficient and
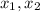 are roots of the equation.
are roots of the equation.
You are given
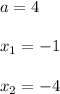
Hence, it is easier to write the quadratic equation in the second form:
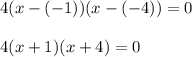
If you myltiply all terms then the equation will be written in the first form: