Question

Given the following students' test scores (95, 92, 90, 90, 83, 83, 83, 74, 60, and 50), identify the mean, median, mode, range, variance, and standard deviation for the sample.

Write a 500-750-word summary and analysis discussing the results of your calculations.
State your results for the sample: the mean, median, mode, range, variance, and standard deviation

Explain which method is best for this data set. Why?
Conduct a one sample T-test and interpret the results (use a population mean of 70).
In what situations would this information be useful?

Answer 1

Mean = 80

Median = 83

Mode = 83

Range = 45

Variance = 214.6667

Standard deviation = 14.65151

Mean method is best for this data set.

The t-test result is population mean does not equal to 70.

Explanation:

Mean is used to measure the central tendency of data which represents the whole data in the best way. It can be found as the ratio of the sum of all the observations to the total number of observations.

⇒
`Mean = (95+92+ 90+ 90+ 83+ 83+ 83+ 74+ 60+ 50)/(10)`

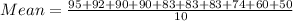
⇒ Mean = 80

Median is the middle observation of given data. It can be found by following steps:

Arranging data in ascending or descending order.

Taking the average of middle two value if the total number of observation is even, and this average is our median.

or, if we odd number of observation then the most middle value is our median.

⇒ Median = ( 5th term + 6th term)÷ 2

⇒ Median = ( 83 + 83)÷ 2 =83

The mode is the observation which has a high number of repetitions (frequency).

⇒ Mode = 83

Standard Deviation is the square root of sum of square of the distance of observation from the mean.

`Standard deviation(\sigma) = \sqrt{(1)/(n)\sum_(i=1)^(n){(x_(i)-\bar{x})^(2)} }`

where,
`\bar{x}` is mean of the distribution.

⇒ Standard Deviation = 14.65151

Variance is a square of the Standard Deviation.

⇒ Variance = 214.6667

Range is the difference between the largest and smallest value.

⇒ Range = Largest Value - Smallest Value

⇒ Range = 95 - 50 = 45

Mean is best representing the given data set since there is no outlier present in our data.

Applying t- test:

Let out hypothesis is:

H₀: μ = 70

H₁: μ ≠ 70

Now,
`t=\frac{\bar{x}-\mu}{(\sigma)/(√(n))}`

Here, μ = Population Mean = 70

`\bar{x}` = Sample Mean = 80

`\sigma` = Standard Deviation = 14.65151

n = 10

Putting all values we get, t = 2.158 with (10 -1) = 9 degree of freedom.

∴ p-value ≈ 0.059

Hence, we reject the Null Hypothesis.

Thus, true mean is not equal to 70.