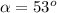Question

Explain how to find the measures of the angles in a right triangle, given the lengths of two sides.

Answer 1

Explanation:

STEP 1:

Find a length of third side.

Use the Pythagorean theorem:

`leg^2+leg^2=hypotenuse^2`

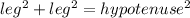
STEP 2:

Use the trigonometric functions:

`sine=(opposite)/(hypotenuse)\\\\cosine=(adjacent)/(hypotenuse)\\\\tangent=(opposite)/(adjacent)`

STEP 3:

Use theorem: the sum of the measures of acute angles of the right triangle is 90°.

Example:

We have the length of legs: a = 3, b = 4.

Let c = hypotenuse.

Use the Pyhagorean theorem:

`c^2=3^2+4^2\\\\c^2=9+16\\\\c^2=25\to c=√(25)\\\\c=5`

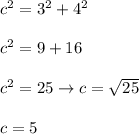
Angle between a and c (β):

Use sine. Therefore b = opposite, c = hypotenuse:

`\sin\beta=(4)/(5)=0.8`

look at the picture

`\beta\approx37^o`

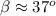
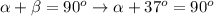`\alpha+\beta=90^o\to\alpha+37^o=90^o` subtract 37° from both sides

`\alpha=53^o`

Answer 2

If you are given two side lengths then you can write an equation using a trigonometric ratio that uses those side lengths, with one of the angle measures as the unknown. Then use the inverse of that trig function to solve for the angle. Once you know one of the angle measures, you can find the other by subtracting the measure from 90 degrees, because the two acute angles in a right triangle are complementary.

Explanation:

EDGE 2021 got a 100%