Answer: (a) 0.000028 (b) 0.001479
Explanation:
Given : Illinois license plates used to consist of either three letters followed by three digits or two letters followed by four digits.
Number of ways to form a licence plate having three letters followed by three digits :-
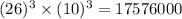
Number of ways to form a licence plate having two letters followed by four digits :-
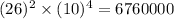
Total number of ways to form a licence plate : 17576000+6760000=24336000
(a) If a license place consists of 7777, then it must belongs to "two letters followed by four digits."
Then, the number of ways to make a license plate having number 7777 will be :_
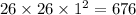
Now, the probability that a randomly chosen plate contains the number 7777 :_
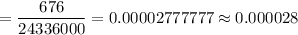
(b) Consider ME as 1 thing.
The number of ways to make a license plate contains the substring ME will be :_

Now, the probability that a randomly chosen plate contains the substring ME :-
