Answer:
maximum at (x,y) = (1/9, 1/27)
minimum at (x,y) = (- 1/9, - 1/27)
Explanation:
The Method of Lagrange Multipliers is used when we need to find a max o min from a f(x,y) subject to a constraint g(x,y); g(x,y)=K (constant)
We can obtain the critical points (maximums and minimums) subject to the constraint by solving the system of equations:
∇f(x,y)=λ∇g(x,y) ; (gradient)
g(x,y)=K
where:
f(x, y) = 4x + 2y
g(x,y)=2x^2 + 3y^2 = 189
Then:
(4,2)=λ(4x,6y)
2x^2 + 3y^2 = 189
---------------------
4=4λx ⇒ x=1/λ
2=6λy ⇒ y=1/3λ
2x^2 + 3y^2 = 189
---------------------
We replace x and y in the third equation:
2*(1/λ)^2+3*(1/3λ)^2=189 / *3λ^2
6+1=567λ^2
λ=
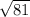
λ=±9
---------------------
λ=+9
(x,y)=(1/9, 1/27) ⇒ f(x,y) >0 ⇒ (x,y) is a maximum
---------------------
λ= -9
(x,y)=(-1/9,- 1/27) ⇒ f(x,y) <0 ⇒ (x,y) is a minimum