Answer:
The bus must be used 21 times a month so that the total monthly cost without the coupon book is the same as the total monthly cost with the coupon book.
Explanation:
This problem can be modeled by two first order functions. One function is the monthly cost without the coupon book, and the other function is the monthly cost with the coupon book.
Monthly cost without the coupon book:
The only thing that the person will spend is the bus fare, that is $1.75. So the cost is:
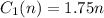
where n is the number of times that the person rode the bus.
Monthly cost with the coupon book:
The person will spend $21 for the book plus the bus fare, that will be $.75. So the cost is:
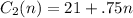
The total monthly cost without the coupon book is the same as the total monthly cost with the coupon book when C1 = C2. So:
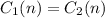
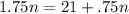
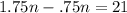

The bus must be used 21 times a month so that the total monthly cost without the coupon book is the same as the total monthly cost with the coupon book.