Question

Find the 2 critical points of the given function and then determine whether it is a local maximum, local minimum, or saddle point. (Order your answers from smallest to largest x, then from smallest to largest y.)

f(x, y) = (x − y)(xy − 9)

Answer 1

Explanation:

Given is a function f in two variables as

`f(x, y) = (x − y)(xy − 9)`

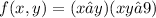
To find critical points of the given function and also to find max, min or saddle point.

Find the partial derivatives

`f(x,y) = x^2y-xy^2-9x+9y`

`f_x=2xy-y^2-9\\f_y =x^2-2xy+9\\f_(xy)  =2x-2y = f_(yx)`

`f_(xx)=2y\\ f_(yy)=-2x`

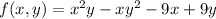
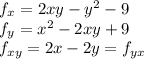
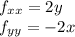
Equate first derivatives to 0

Adding fx and fy we get

`x^2-y^2 =0\\`

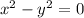
x=±y

Only real roots are (x,y) =(3,3) and (-3,-3)

`D(3,3)=f_(xx)(3,3) f_(yy)(3,3)-f_(xy)^2(3,3) \\=-36-0<0`

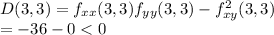
(3,3) is a saddle point

`D(-3,-3) = -36<0`

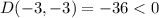
(-3,-3) is also a saddle point.