Question

Find x such that 3^x = 27 mod 32 (b)

Answer 1

The value of x is 11.

Explanation:

Consider the provided information.

It is given that
`3^x = 27 mod\ 32`

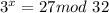
We know that:

`3^4=81`

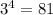
Now if we divide the number 81 with 32 it will gives us remainder 17.

This can be written as:

`3^4\equiv 17(mod\ 32)`

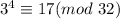
Now use the property:
`a^n\equiv b^n(mod\ m)`

`(3^4)^2\equiv 17^2(mod\ 32)`

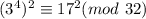
17²=289, if we divide 289 with 32 it will gives us remainder 1, thus.

`3^8\equiv 1(mod\ 32)`

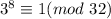
Multiply both the sides by 3³.

`3^8* 3^3\equiv 3^3(mod\ 32)`

`3^(11)\equiv 27(mod\ 32)`

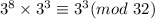
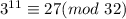
Hence, the value of x is 11.