Question

Find three positive numbers whose sum is 18 and whose product is maximal. (Enter your answers as a comma-separated list.)

Answer 1

Explanation:

Given that three positive numbers have sum 18.

Let the numbers be
`x,y, 18-x-y`

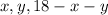
Then product

`f(x,y) =xy(18-x-y) = 18xy-x^2y-xy^2`

To find maxima, let us use partial derivaties

`f_x = 18y-2xy-y^2\\f_y =18x-x^2-2xy\\f_xx= -2x\\f_yy=-2y\\f_xy = 18-2x = f_yx`

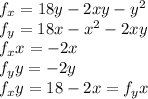
Equate I derivatives to 0

Solving the two linear equations we get solution as

(6,6)

Hence maximum when x =y=z=6

i.e. when all numbers are equal to 6.