Question

Find an equation of the line that passes through the point (3, 2) and is perpendicular to the line 8x + 7y − 9 = 0. (Let x be the independent variable and y be the dependent variable.)

(Please show each step and thank you for your time)

Answer 1

The required equation of line is
`7x-8y-5=0`.

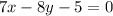Explanation:

Given : The point (3, 2) and is perpendicular to the line
`8x+7y-9 = 0`.

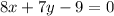To find : An equation of the line that passes through the point ?

Solution :

We know that,

When two lines are perpendicular then one slope is negative reciprocal of another slope.

The slope of
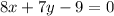`8x+7y-9 = 0` line is

Write the equation in slope form,

`7y=-8x+9`

`y=-(8)/(7)x+(9)/(7)`

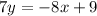
The slope is
`-(8)/(7)`.

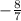The slope of required equation is
`m=-((1)/(-(8)/(7)))=(7)/(8)`

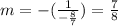
The point is
`(x_1,y_1)=(3,2)`.

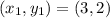The equation of required line is
`y-y_1=m(x-x_1)`

Substitute the value,

`y-2=(7)/(8)(x-3)`

`8(y-2)=7(x-3)`

`8y-16=7x-21`

`7x-8y-5=0`

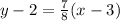
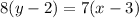
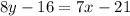
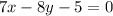
Therefore, the required equation of line is
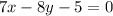`7x-8y-5=0`.

Answer 2

1) first we have to find the slope of the linear function we have to find. As we know, it is perpendicular to the function 8x+7y-9=0. So that means that the slope of our function has to be opposite and inverse to the function we are given. To know the slope of the function we have to isolate Y.

8x+7y-9=0
7x=-8x+9
X=-8/7x+9/7

So the slope of this function is -8/7, which means that the slope of our function is 7/8.

So far we know that:
Y=7/8x+B

2) now we have to find the value of the intersection with Y (B). In order to do this we use the point (3;2) and supplant it on the equation.

2 = 7/8 . 3 + b

2 = 21/8 + b

2 - 21/8 = b

-5/8 = b

So the equation is:

Y = 7/8 x - 5/8

I hope you find my answer helpful