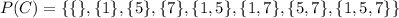Answer:
(a)
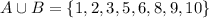
(b)
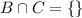
(c)
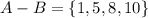
(d)
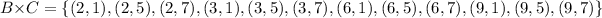
(e)
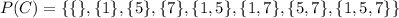
Explanation:
Given information:
A, B and C are three sets:
A={1,3,5,6,8,10}, B = {2,3,6,9}, C = {1,5,7}
A set contains distinct elements.
(a)
We need to find the set AUB. In this set all elements of A and B are included.
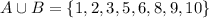
(b)
We need to find the set B∩C. In this set all common elements of B and C are included.
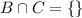
It is an empty set because there is no common element in set B and C.
(c)
We need to find the set A-B. In this set all elements of A are included excluding the common elements of A and B.
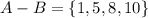
(d)
We need to find the set BxC.
BxC is defined as
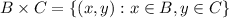
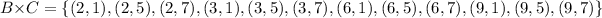
(e)
We need to find the set P(C). It is a power set of C. It is the collection of all subsets of set C.