Question

In the following you may leave your answer as a binomial or multinomial coefficient. In each case give a brief justification for your answer. (a) How many ways are there to give 5 apples and 7 bananas to 12 people assuming that each person gets a piece of fruit? (b) How many ways are there to give 7 apples to 13 people with no restrictions on the number of apples a person can get?

Answer 1

Answer: a) 792 ways b) 13⁷.

Explanation:

Since we have given that

Number of apples to be given = 5

Number of bananas to be given = 7

Number of people = 12

So, Number of ways that each person gets a pieces of fruit is given by

`(12!)/(7!* 5!)\\\\=792\ ways`

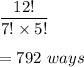
b) If the number of people = 13

Number of apples to be given = 7

So, Number of ways would be

`13* 13* 13* 13* 13* 13* 13\\\\=13^7`

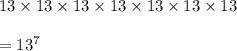
Hence, a) 792 ways b) 13⁷.