Answer: (a) 676000
(b) 468000
Explanation:
We know that the total number of digits in the number system from 0 to 9= 10
The total number of letters in English alphabet (Only upper case) from A to Z = 26
Given : In a certain state, license plates cach consist of 2 letters followed by 3 digits.
(a) If repetition is allowed , then the total number of different license plates there are :-
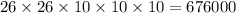
hence, the number of different license plates = 676000
(b) If repetition is not allowed , then the total number of different license plates there are :-
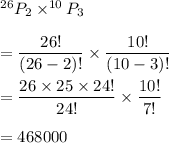
Hence, the number of different license plates are there that have no repeated letters or digits=468000