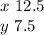Question

A solution containing 12% alcohol is to be mixed with a solution containing 4% alcohol to make 20 gallons of solution containing 9% alcohol. a. Identify the unknowns to be evaluated in the above given problem. b. Develop the system of simultaneous equations which represent the above problem. c. Find the solution of the system of simultaneous equation you have developed in part (b), using a matrix method

Answer 1

Explanation:

Given that a solution containing 12% alcohol is to be mixed with a solution containing 4% alcohol to make 20 gallons of solution containing 9% alcohol.

Let x gallons of 12% alcohol be mixed with y gallons of 4% alcohol.

Total gallons
`= x+y = 20`

Alcohol content in the total mixture
`= 0.12x+0.04y =9% of x+y`

`0.12x+0.4y=0.09(20)\\12x+4y = 180`

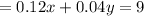
b) Two equations are

`x+y = 20\\12x+4y = 180`

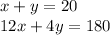
c) This is of the form Ax = B

where A =
`\left[\begin{array}{ccc}1&1\\12&4\end{array}\right]`

Inverse is
`(1)/(4-12) \left[\begin{array}{ccc}4&-1\\-12&12\end{array}\right]\\=(-1)/(8) \left[\begin{array}{ccc}4&-1\\-12&12\end{array}\right]\\`

Solution set is A inverse *B

=
`x \    12.5\\y  \     7.5`