Question

CarcuratOS 11.A credit card charges an annual rate of 18% compounded monthly. This month's bill is Rs. 35,000... Suppose that you keep paying Rs. 5000 each month. How long will it take to pay off the bill? What is the total interest paid during that period? 111Over 10 years a bond costing Rs. 3000 increases in value to Rs. 5372.54. Find the effective annual rate.

Answer 1

FIRST QUESTION

It will pay the bill after 7.45 = rounding 8 months, being the last payment less than 5,000

The total interest for the period will be 2,263.04

SECOND QUESTION The rate will be 6%

Explanation:

for the first part, we should calculate the time it takes to an ordinary annuity of 5,000 to have a present value of 35,000 at discount rate of 18%

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 5,000

time n

rate 0.015

PV $35,000.0000

`5000 * (1-(1+0.015)^(-n) )/(0.015) = 35000\\`

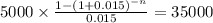
We work out the formula:

`(1+0.015)^(-n)= 1-(35000*0.015)/(5000)`

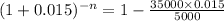
We solve the right side of th formula

and then apply logarithmics properties:

-n = -7.450765527

n = 7.45

It will pay the bill after 8 months.

Total Interest: we will build the loan schedule:

Bill Interest Cuota&Amortization

1 35000 525& 5000 4475

2 30525 457.88 5000 4542.12

3 25982.88 389.74 5000 4610.26

4 21372.62 320.59 5000 4679.41

5 16693.21 250.4 5000 4749.6

6 11943.61 179.15 5000 4820.85

7 7122.76 106.84 5000 4893.16

8 2229.6 33.44 2263.04 2229.6

Total 2263.04 37263.04 35000

The total interest for the period will be 2,263.04

Second question we will solve for the rate at which a capital of 3,000 returns 5,372.54 after 10 years

`Principal \: (1+ r)^(time) = Amount`

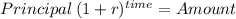
Principal 30,00.00

Amount = 5,372.54

time 10.00

rate ?

`3,000 \: (1+ r)^(10) = 5,372.54`

`r = \sqrt[10]{5,372.54/3,000} - 1`

r = 0.059999939 = 0.06 = 6%